Глава 6. Удары от бортов и абриколи

Глава представляет вам почти всё, что вам необходимо знать о выполнении ударов от бортов и абриколей, где шары с пользой для вас отражаются от бортов. Если вы владеет умением выполнять широкий спектр ударов от бортов и абриколей, то вы сможете выйти из множества трудных ситуаций и выиграть много больше игр.
Раздел 6.01 Введение
На Рисунке 6.1 показана терминология ударов от бортов.
Биток попадает по прицельному шару с углом резки (или без него) и направляет прицельный шар на борт.
Угол сближения (АКА угол падения, АКА входящий угол) - это угол, который образует путь прицельного шара с перпендикуляром к борту.
Угол мал для более прямых попаданий в борт, и велик для ударов по касательной.
На рисунке изображён угол падения около 40°.
Угол отскока (АКА угол отражения АКА исходящий угол) - это угол, под которым прицельный шар покидает борт после соударения.
Углы падения и отражения измеряются в точке контакта шара с бортом. Эта точка находится на бортовой канавке.
Бортовая канавка - это воображаемая линия, проходящая параллельно борту на расстоянии в половину диаметра шара.
Бортовая канавка - это линия, вдоль которой катится шар при скатывании вдоль борта (например, при резке бортового шара).
Иногда эти линии видны на очень изношенных столах.

Когда биток отражается от борта перед контактом с прицельным шаром (смотри Рисунок 6.2), такой удар называется абриколь.
Иногда такие удары - это единственный способ забить шар и довольно часто единственный вариант игры при хорошо выполненном отыгрыше.
К счастью, все методы, используемые для прицеливания обычного удара от борта, также могут быть использованы для планирования абриколей,
хотя для абриколей у вас больше возможностей для контроля вращения битка во время контакта битка с бортом.

Существует масса различных методов для прицеливания ударов от бортов и абриколей. Существуют методы, основанные на базовых принципах геометрии. Наиболее общие и практические методы представлены в Разделах 6.02 и 6.03 и включают в себя следующее:
- Метод равных отрезков
- Расширенный метод равных отрезков
- Метод параллели, проведённой через середину отрезка
- Метод зеркального отражения
- Метод равных отрезков для абриколей
В Разделе 7.06 представлены некоторые дополнительные более сложные методы, полезные при планировании ударов от нескольких бортов.
В Принципе 6.1 говорится о геометрическом предположении, на котором основаны все методы прицеливания ударов от бортов.
Это тот же самый принцип, в котором говорится о поведении лучей света, отражённых от зеркала: "Угол падения равен углу отражения".
(Если вы изучали физику в школе, то возможно вы смутно помните данную концепцию).
К сожалению, это предположение верно для бильярдного шара только тогда, когда шар ударяется о борт со средней скоростью и без бокового винта (смотри Раздел 6.04).
Тем не менее, методы прицеливания для ударов от бортов и абриколей, основанные на принципе отражения, всё ещё применяются, поскольку
они обеспечивают хороший ориентир для прицеливания, в который можно внести коррективы на основе вашего опыта и интуиции.
Даже если необходимые коррективы не являются интуитивно очевидными для вас, или у вас нет полной уверенности в правильности своей интуиции,
вы можете спланировать коррективы, основываясь на принципах скорости удара и применяемого винта, представленных в Разделах 6.4, 6.5 и 6.6.
Как правило, угол отражения для удара от борта равен углу падения (смотри Рисунок 6.1).
- Это утверждение неверно для сильных и тихих ударов, для случаев, когда прицельный шар стоит близко к борту (смотри Раздел 6.04), для ударов с боковым вращением (смотри Раздел 6.05) и для ударов на резке (смотри Раздел 6.06).
Как показано на Рисунке 6.3, если бы вы могли использовать зеркало, чтобы помочь вам прицелить удар от борта или абриколь,
вам бы было очень легко визуализировать идеальное направление прицеливания. Вы просто должны перемещать зеркало вдоль бортовой канавки, пока не увидите отражение целевой лузы.
Если вы направите прицельный шар со средней скоростью в отражение в зеркале, то прицельный шар, отразившись от борта попадёт точно в лузу (не забудьте убрать зеркало во время удара :).
К сожалению, использование зеркала при прицеливании запрещено правилами, так как вам не разрешается использовать для прицеливания любое специальное оборудование.
Если вы используете зеркало для тренировок, то не забывайте убирать его перед ударом (особенно если вы суеверны или если одолжили зеркальце у супруги).

Раздел 6.02 Методы прицеливания ударов от бортов
Основной метод прицеливания ударов от бортов показан на Рисунке 6.4.
Он называется Метод равных отрезков и основан на Принципе 6.1.
Чтобы использовать данный метод, перемещайте точку взаимодействия с бортом вдоль борта пока не добьётесь равенства отрезков, как показано на рисунке.
Отрезки можно откладывать как на борту, от которого будет отражаться прицельный шар, так и на противоположном борту, прилегающем к целевой лузе.
Как указано в Принципе 6.2, должно быть равенство расстояний между точкой проекции линии прицеливания и точкой взаимодействия с бортом и между точкой
взаимодействия с бортом и целевой точкой.
Обратите внимание, что все точки находятся на бортовых канавках, что очень важно для точного измерения расстояний.

Для удара от борта со средней скоростью, без использования винтов, следующие расстояния должны быть равны:
- между точкой проекции линии прицеливания и точкой взаимодействия с бортом
- между точкой взаимодействия с бортом и целевой точкой (смотри Рисунок 6.4 и NV 6.1)
- Этот принцип является прямым следствием Принципа 6.1.
- Равенство отрезков не будет соблюдаться для быстрых или медленных скоростях, или в случае близости прицельного шара к борту (смотри Раздел 6.04), или в случае использования винтов (смотри Раздел 6.05) или для ударов на резке (смотри Раздел 6.06).
NV 6.1 Метод равных отрезков
При использовании Метода равных отрезков сначала следует воспользоваться собственной интуицией,
чтобы определить где (по вашему мнению) должна находиться точка взаимодействия с бортом.
Теперь вы имеет предполагаемую линию прицеливания, которую вы может спроецировать на нижний борт (например, с помощью кия) для определения точки проекции линии прицеливания.
Далее мы проверяем, чтобы расстояние от целевой точки до точки проекции линии прицеливания было в два раза больше, чем
расстояние от целевой точки до точки взаимодействия с бортом.
Как показано на Рисунке 6.4, короткое расстояние можно легко измерить вдоль борта или, в качестве альтернативы, вы можете сравнить
расстояние от целевой точки до точки взаимодействия с бортом с расстоянием от точки взаимодействия с бортом до точки проекции линии прицеливания.
Если отрезки не равны, вам нужно скорректировать прицеливание.
Как показано на Рисунке 6.5 если ваша первая догадка неверна и точка взаимодействия с бортом смещена слишком вправо, то отрезки не будут равны и вам необходимо сместить
точку взаимодействия с бортом влево для того, чтобы уравнять отрезки и углы падения и отражения от борта.
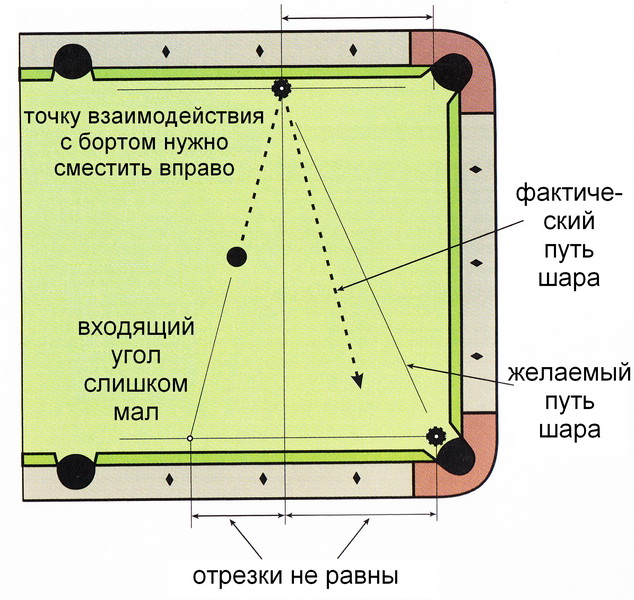
На Рисунке 6.6 показано, что произойдёт, если вы ошибётесь в другом направлении.
И снова вы должны перемещать точку прицеливания (в данном случае - вправо), пока отрезки ни станут равными.
Эта техника требует в первое время немного практики, но когда вы начнёте лучше прицеливать удары от бортов, ваши первоначальные догадки по поводу точки взаимодействия
с бортом будут достаточно точными и требовать, возможно, лишь небольших поправок.

При прицеливании ударов от бортов вы должны иметь возможность оценить расстояния вдоль бортов.
К счастью, чтобы помочь нам производители бильярдных столов предоставляют в наше распоряжение алмазы.
(Кроме того, алмазы круто смотрятся на столе).
Алмазы равномерно распределены вдоль каждого борта - по три штуки между каждыми лузами.
В дополнение к видимым алмазам вы также должны знать о местах расположения алмазов в лузах.
Для средней лузы воображаемый алмаз находится в центре лузы на линии с другими алмазами.
Однако для угловой лузы существует два различных мнимых алмаза, расположение которых зависит от того, вдоль какого борта вы измеряете расстояние.
На Рисунке 6.7 показаны эти места расположения.
Алмазы угловой лузы расположены на пересечении линий, образованных другими алмазами, с линиями, образованными краями прилегающих бортов.
При использовании алмазов для точного измерения расстояний вдоль бортов эти места расположения имеют важное значение.

На Рисунке 6.8 показано, что расположение целевой точка для угловой лузы не точно совпадает с расположением воображаемого алмаза.
Для точного прицеливание удара от борта, это смещение будет оказывать влияние на измерение бортовых расстояний.
Для упрощения задачи прицеливания в первое время можно делать допущение, что целевая точка совпадает с воображаемым алмазом.
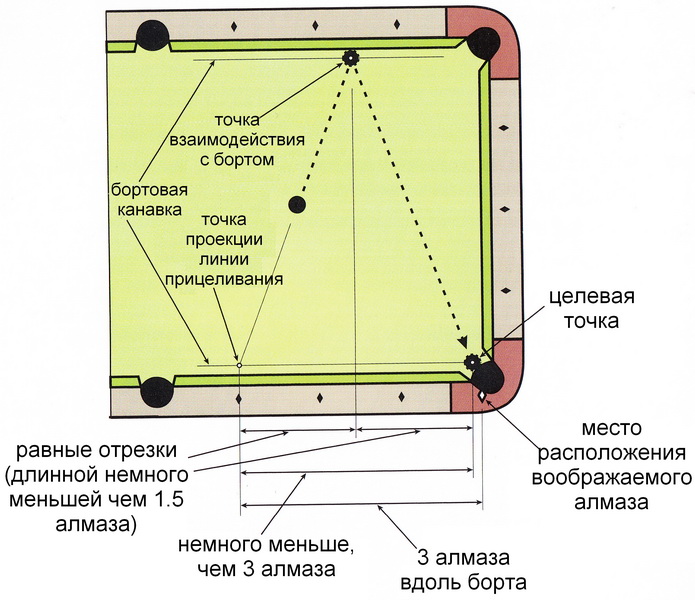
Для примера, изображённого на Рисунке 6.8, точка проекции линии прицеливания находится на расстоянии ровно трёх алмазов от воображаемого алмаза угловой лузы.
Таким образом, вы определили, что точки взаимодействия с бортом расположена на расстоянии полтора алмаза от целевой точки, стало быть вы попадёт
достаточно близко к желаемой целевой точке.
Измеряя более точно, точка проекции линии прицеливания находится немного ближе к целевой точке, чем на расстоянии 3 алмаза.
Таким образом, как показано на рисунке, расстояние от точки взаимодействия с бортом до точки проекции линии прицеливания будет немного меньше, чем полтора алмаза.
При ударе средней силы, шар отразится от борта точно в центр лузы, как показано на рисунке.
Принцип 6.3 обобщает а Рисунок 6.9 иллюстрирует очень важный момент в использовании алмазов.
Они должны использоваться в целях измерения расстояний, а не как точки для прицеливания.
Целевая точка, точка взаимодействия с бортом и точка проекции линии прицеливания должны быть расположены на бортовой канавке, на которую проецируются алмазы.
Когда вы целитесь, вы целитесь в точку взаимодействия с бортом, а не в точку расположения алмаза.
На Рисунке 6.9 показан путь шара, который мы имеем, если целиться напрямую в алмаз.
Шар даже близко не попадёт в лузу.
Путь битка, полученный в результате прицеливания в точку взаимодействия с бортом, также неидеален - шар попадёт не в центр лузы.
Это произойдёт потому, что центр лузы находится немного левее воображаемого алмаза угловой лузы (смотри Рисунок 6.8).
Точка взаимодействия с бортом должна быть сдвинута немного левее второго алмаза (но не настолько сильно, как при прицеливании прямо в алмаз)
для выравнивания расстояний между точкой проекции линии прицеливания, точкой взаимодействия с бортом и целевой точкой центра лузы.
При прицеливании удара от борта используйте алмазы для измерения расстояний вдоль борта, но целиться надо в точки на бортовой канавке, на которые проецируются алмазы (смотри Рисунок 6.9).
- В некоторых методах прицеливания ударов от множества бортов (например Система "5" или Система Плюс, иногда использующиеся в Трёхбортном Карамболе), вам надо целиться именно в алмазы (смотри TP 7.2 в Разделе 7.06).

Метод равных отрезков, представленный выше, может также использоваться для ударов, когда линия прицеливания, спроектированная назад, выходит за пределы стола.
На Рисунке 6.10 показан такой случай.
Метод прицеливания, применяемый для таких ударов, на самом деле такой же как Метод равных отрезков.
Но когда вам нужно измерить расстояние за пределами стола, я называю этот способ Расширенным методом равных отрезков.
Как и прежде, вы смещаете точку взаимодействия с бортом пока не добьётесь равенства отрезков, проведённых между
точкой проекции линии прицеливания, точкой взаимодействия с бортом и целевой точкой.
В NV 6.2 показано как этот метод применяется на практике.

NV 6.2 Расширенный метод равных отрезков
Альтернативой Методу равных отрезков служит метод показанный на Рисунке 6.11 и изложенный в Принципе 6.4.
Он называется Метод параллели, проведённой через середину отрезка, и он также основан на Принципе 6.1 (смотри TP 6.1).
Этот метод концептуально немного сложнее, чем Метод равных отрезков, но он прост и не требует догадок и корректировок относительно точки взаимодействия с бортом.
Для использования метода, сперва представьте отрезок между текущим положением прицельного шара (точка А) и целевой лузой (точка B).
Далее разделите отрезок АВ пополам, чтобы найти середину отрезка.
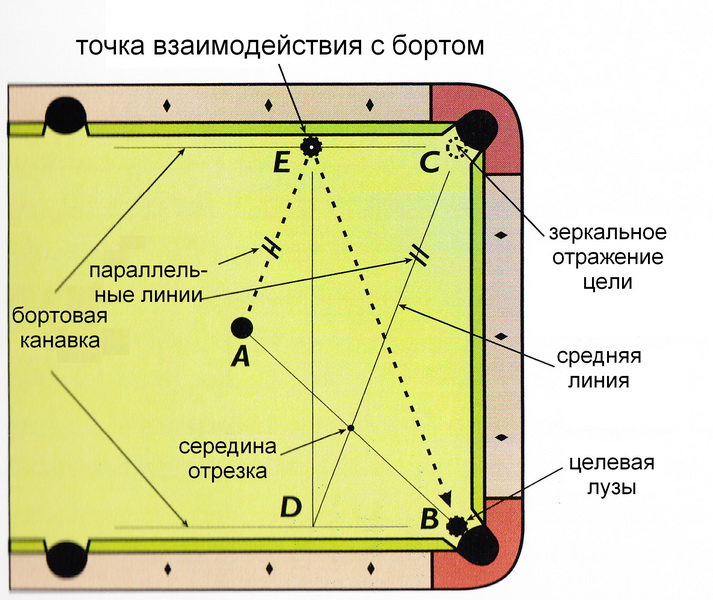
Затем представьте себе линию (например, при помощи кия) через эту середину отрезка и зеркальное отражение целевой лузы на другой стороне стола (точкой С).
Эта линия (отрезок DC) обозначена на рисунке как "средняя линия".
Она задаёт направление, по которому прицельный шар должен приближаться к борту из точки А, чтобы отразиться от борта (в точке взаимодействия с бортом Е)
и попасть в лузу (в точку В). То есть, прямая АЕ параллельна средней линии DC.
Точка взаимодействия с бортом (точка Е) может быть найдена с помощью проекции точки D на противоположный борт (при построении может пригодиться помощь алмазов).
В нашем примере точка D (и как следствие точка Е) находится на расстоянии чуть более полутора алмазов от угловой лузы.
Этот метод включает в себя несколько шагов и требует умения визуализировать различные линии и находить середину отрезка, но
он может быть хорошей альтернативой Методу равных отрезков.
Для исполнения удара от борта со средней скоростью и без использования винтов, линия прицеливания должна быть параллельна линии, проходящей через зеркальное отражение целевой лузы и середину отрезка, соединяющего точку расположение прицельного шара и целевую лузу (смотри Рисунок 6.11 и NV 6.3).
- Этот принцип является прямым следствием Принципа 6.1.
- Этот принцип неверен для быстрых или медленных скоростях, или в случае близости прицельного шара к борту (смотри Раздел 6.04), или в случае использования винтов (смотри Раздел 6.05) или для ударов на резке (смотри Раздел 6.06).
NV 6.3 Пример применения Метода параллели, проведённой через середину отрезка
Далее
Chapter 6. Bank and Kick Shots

Chapter presents most of what you ever wanted or needed to know about executing bank shots and kick shots, where you bounce balls off rail cushions to your advantage. If you have the ability to make wide variety of bank and kick shots, you will be able to get out of many difficult situations and win many more games.
Section 6.01 Introduction
Figure 6.1 illustrates bank shot terminology.
The cue ball strikes the object ball, with or without a cut angle, and drives the object ball to the rail.
The approach angle (aka angle of approach, angle of incidence, or entering angle) is the angle the object-ball path forms with the perpendicular to the rail.
The angle is small for balls hit more directly at the rail, and large for balls striking at a glancing angle.
In the figure, the approach angle is about 40°.
The rebound angle (aka angle of rebound, angle of reflection, or leaving angle) is the angle at which the object ball leaves after striking the rail.
The approach and rebound angles are measured relative to the position the ball is in when it is in contact with the rail, in the rail groove, AKA rail gutter.
The rail groove is the imaginary line adjacent to the rail, locating the center of the banked ball when it is in contact with the rail.
The rail groove is the line upon which a ball rolls when it travels down a rail (e.g., with a rail cut shot).
Sometimes, the rail groove is visible on tables as a result of excessive use.

When the cue ball is banked off the rail before contacting the object ball (see Figure 6.2), the shot is called a kick shot.
These shots are sometimes the only way to pocket a ball, and can often be the only reply to a well executed safety.
Fortunately, all of the methods used to aim normal bank shots can also be used to plan kick shots; although,
with kick shots you have more control over the spin and English of the ball hitting the rail (the cue ball).

There are many different methods for aiming bank and kick shots. There are based on basic geometry principles. The most basic and practical methods are presented in Section 6.02 and Section 6.03, and they include the following:
- equal rail-distance bank shot
- equal extended-rail-distance bank shot
- parallel midpoint-line bank shot
- mirror-image kick shot
- equal separation-distance kick shot
Section 7.06 presents some additional, more complicated, methods useful in planning multiple-rail bank and kick shots.
Principle 6.1 summarizes the geometric assumption upon which all of the bank and kick-shot aiming methods are based.
It is the same principle that governs how rays of light reflect off mirrors: "The angle of incidence equals the angle of reflection."
(If you had a high school physics class, maybe you vaguely remember this concept).
Unfortunately, this assumption is true for a pool ball bouncing off a rail only when the ball hits the rail with medium speed and no sidespin (see Section 6.04).
However, the aiming methods for bank and kick shots that are based on the reflection principle are still useful because
they provide good aiming references from which you can make adjustments derived from your experience-based intuition.
Even if the required adjustments are not intuitively obvious to you, or you are not totally confident with your intuition,
you can plan the adjustments based on the speed and spin principles presented in Section 6.4, Section 6.05, and Section 6.06.
Generally, a bank-shot rebound angle (the angle of reflection) is the same as the approach angle (the angle of incidence) (see Figure 6.1).
- This statement is not true at fast or slow speeds, or when the object ball is close to the rail (see Section 6.04), with English (see Section 6.05), or for cut shots (see Section 6.06).
As illustrated in Figure 6.3, if you could use a mirror to help you aim bank and kick shots, it would be very easy to visualize the ideal required aiming-direction.
You would simply need to move the mirror along the rail (in the rail groove) until you could see the target pocket in the reflection.
If you shot the object ball at the image in the mirror with medium speed, the object ball would
bounce off the rail into the pocket (provided the mirror were removed during the shot).
Unfortunately, using a mirror as an aiming aid is illegal, because you are not allowed to use any special equipment as an aiming aid.
If you are using a mirror for practice, don’t forget to have someone remove the mirror before you shoot
(especially if you are superstitious, or if you borrowed a "special" mirror from your spouse).

Section 6.02 Bank-shot aiming methods
The most basic method for aiming bank shots is illustrated in Figure 6.4.
It is called the equal rail-distance method and is based on Principle 6.1.
To use the method, you move your rail-impact aim point along the bank rail until the distances shown in the figure are equal.
The distances are measured along the bank rail or along the rail opposite from the bank rail, adjacent to the target pocket.
As summarized in Principle 6.2, the distances that are equal are between the projected aiming line point and the rail-impact aim point, and
between the rail impact aim point and the target point.
Note that all of the points are defined along the rail grooves, which is important when trying to measure distances accurately.

To make a medium-speed bank shot with no English, the rail distances between the projected aiming-line point, rail-impact aim point, and target point must be equal (see Figure 6.4 and NV 6.1).
- This principle is a direct consequence of Principle 6.1.
- The distances are not equal at fast or slow speeds, or when the object ball is close to the rail (see Section 6.04), with English (see Section 6.05), or for cut shots (see Section 6.06).
NV 6.1 Equal-distance bank method
To use the equal rail-distance method, first use your intuition to determine where you think the rail-impact aim point should be.
This defines the estimated aiming line, which you can project to the bottom rail (e.g., using the cue stick) to define the projected aiming-line point.
Then, check to see if the distance from the target point to the projected aiming-line point
is twice the distance from the target point to the rail-impact aim point.
As shown in Figure 6.4, the shorter distance can be easily measured along either rail or, as an alternative to measuring the distance
from the target point to the rail-impact aim point, you could measure the distance from the rail-impact aim point to the projected aiming-line point.
If the distances are not equal, you need to adjust your aim.
As illustrated in Figure 6.5, if your first guess for the rail-impact aim point if too far to the right, the rail distances
will not be equal and you will need to move your aim point to the left, to equalize the rail distances and the approach and rebound angles.
Figure 6.6 shows what happens if your guess is in error in the other direction.
Again, you must move the aim point (in this case, to the right) until the rail distances are equal.
This technique takes a little practice at first, but as you get better with aiming bank shots, your initial guess will
be fairly close, and might require only a small adjustment to equalize the distances.
NV 6.1 shows the equal rail-distance method being used in practice.


With all banking methods, you need to be able to estimate distances along the rails.
Fortunately, the billiard table manufacturers provide us with the diamonds to help.
(The diamonds also look cool on the table).
The diamonds are equally spaced along each rail, with three between each pocket.
In addition to the visible diamonds on the rails, you must also be aware of the diamond locations corresponding to the pockets.
For a side pocket, the imaginary diamond is centered in the pocket in-line with the other diamonds.
However, for a corner pocket there are two different imaginary diamond locations depending upon the rail along which you are measuring.
Figure 6.7 illustrates these locations.
The corner-pocket diamonds are located in-line with the other diamonds, centered on the edge of the adjacent rail.
When using the diamonds to accurately measure distance along a rail to a target point in the pocket, these locations are important.

Figure 6.8 illustrates how a typical corner-pocket target point is not exactly aligned with the imaginary diamond location.
To aim the bank shot precisely, this misalignment would have an impact on how you measure the rail distances.
To simplify things when first using a banking method to aim corner-pocket shots, you might
just assume that your target point is aligned with the appropriate imaginary diamond.
For example, in Figure 6.8 the projected aiming-line point is exactly three diamonds away from the imaginary corner-pocket diamond.
Therefore, you would predict the required rail-impact aim point to be one and a half diamonds from the target,
and you would come fairly close to the desired target point.
Measuring more accurately, the projected aiming line point is actually a little less than three diamonds away from the target.
Therefore, the rail impact aim point should be a little less than one and a half diamonds from the projected aim point, as shown in the figure.
With medium speed, the ball would rebound directly into the pocket center, as shown.

Principle 6.3 summarizes and Figure 6.9 illustrates a very important point concerning how to use the diamonds.
They should be used for measurement purposes only, and not as aiming points.
The target point, rail-impact aim point, and projected aiming-line point need to be located in the rail grooves adjacent to the diamonds.
When you aim your shot, you aim directly at the rail-impact point, not at the diamond adjacent to the point.
Figure 6.9 shows the path the ball takes if you aim directly at the diamond.
The ball does not even come close to going into the pocket.
The ball path resulting from aiming at the equal distance rail-impact point shown is also not perfect—the ball does not enter the center of the pocket.
This is because the center of the pocket is a little to the left of the imaginary corner-pocket diamond (see Figure 6.8).
The rail-impact aim point would need to be moved a small amount to the left of the second diamond
(but not near as far left as the diamond aiming line would suggest) to equalize the distances between the projected aiming-line point,
the rail-impact aim point, and the pocket-center target point.
When lining up basic bank-shot geometry; use the diamonds to measure rail distances, but aim to and from points in the rail grooves adjacent to the diamond locations (see Figure 6.9).
- In some multirail banking methods (e.g., the 5-System and Plus System sometimes used in three-cushion billiard games), you do aim directly at the diamonds (see TP 7.2 in Section 7.06).

The equal rail-distance method presented above can also be used for shots where your aiming-line direction, when projected back, extends beyond the table.
Figure 6.10 illustrates such a case.
The method for this type of shot is really the same as the equal rail-distance method.
But when you need to measure beyond the table, I call the technique the equal extended-rail-distance bank method.
As before, you move your rail-impact aim point until the distances between the projected aiming-line point, rail-impact aim point, and target point are equal.
NV 6.2 shows how the method is used in practice.

NV 6.2 Equal extended-rail-distance bank method
An alternative to the equal rail-distance method presented above is illustrated in Figure 6.11 and summarized in Principle 6.4.
It is called the parallel midpoint-line bank method, and it is also based on Principle 6.1 (see TP 6.1).
It is conceptually a little more complicated than the equal rail-distance method, but it is straightforward
and does not require trial and error with an initial guess and adjustments.
To use the method, first imagine a line between the current object-ball position (point A) and the desired target-location (point B).
Next, bisect this line (line AB) to find the midpoint.
Then, imagine a line (e.g., by using the cue stick) through this midpoint, and the mirror image of the target ball on the other side of the table (point C).
This line (line DC) is labeled as the "midpoint line" in the figure.
It defines the direction at which the object ball needs to approach the rail from point A to rebound off the rail at the rail-impact point
(point E) and be pocketed at point В (i.e., line AE is parallel to the midpoint line).
The rail-impact aim point (point E) can be found by projecting the midpoint line to the rail adjacent to the target (point D).
The aim point (point E) is directly across from point D and can be located using the diamonds.
In this case, point D, and therefore point E, is a little more than one and a half diamonds from the corner pocket.
This method involves more steps and requires that you visualize various lines and the midpoint of a line,
but it can be a good alternative if you dislike the equal rail-distance method.

To make a medium-speed bank shot with no English, the aiming line must be parallel to the line connecting the midpoint between the ball and the target, and the mirror image of the target (see Figure 6.11 and NV 6.3).
- This principle is a direct consequence of Principle 6.1 (see TP 6.1).
- The principle is not valid at fast or slow speeds, or when the object ball is close to the rail (see Section 6.4), with English (see Section 6.05), or for cut shots (see Section 6.06).
NV 6.3 Parallel midpoint-line bank method example
