Глава 6. Удары от бортов и абриколи (2)
Раздел 6.03 Методы прицеливания абриколей
Абриколь - это удар, когда биток, отразившись от борта, попадает в прицельный шар.
Если прицельный шар находится близко к лузе, как показано на Рисунке 6.12, можно использовать метод прицеливания, представленный в предыдущем разделе с тем лишь отличием,
что вы рассчитываете путь битка, а не прицельного шара.
Основным отличием является то, что у вас больше контроль над битком с помощью боковых винтов.
Хорошей новостью является тот факт, что вам не нужно беспокоится об эффектах резки (смотри Раздел 6.06).
Тем не менее, вы должны быть очень осторожны, чтобы нечаянно ни придать битку бокового вращения (смотри Раздел 6.05).

Для абриколей, где прицельный шар находится недалеко от борта, от которого будет отражаться биток, применяются следующие методы.
Первый метод под названием Метод зеркального отражения изображён на Рисунке 6.13 и приведён в Принципе 6.5.
Для использования этого метода, вам надо всего лишь представить зеркальное отображение прицельного шара, отражённого от бортовой канавки
и целиться в воображаемый (зеркально-отражённый) шар.
Зеркально-отражённый шар трудно визуализируется, когда прицельный шар находится далеко от борта, но если он стоит близко, то данный метод достаточно прост в применении.
Когда вы научитесь хорошо визуализировать зеркально-отражённый шар, вы даже сможете спланировать желаемый угол резки прицельного шара, направляя биток
в воображаемый шар с необходимой резкой.
На Рисунке 6.14 показано, как это сделать.
Обратите внимание, что направление угла резки зеркально "перевернулось".
Для забития прицельного шара в лузу биток должен попасть по прицельному шару правее центра.
В зеркальном отражении вы должны целиться левее центра воображаемого шара с таким же количеством резки.

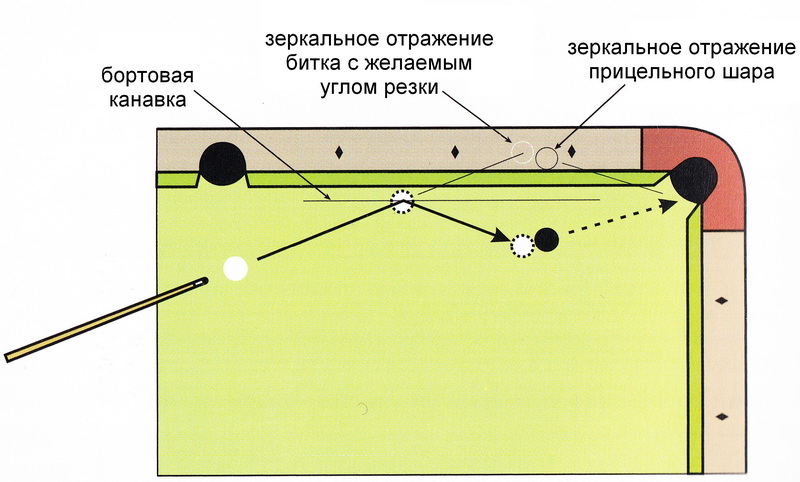
Для абриколя (сила удара средняя; без винтов) вы можете целиться в зеркальное отражение прицельного шара, отражённого от бортовой канавки (смотри Рисунки 6.13, 6.14 и NV 6.4)
- Этот принцип является прямым следствием Принципа 6.1.
- Вам нужно будет внести коррективы в прицеливание при использовании тихих и сильных ударов (смотри Раздел 6.04) и винтов (смотри Раздел 6.05).
NV 6.4 Метод зеркального отражения

Другой метод прицеливания абриколей показан на Рисунке 6.15.
Он именуется Методом равных отрезков для абриколей.
Он применяется по бОльшей части так же как и Метод равных отрезков для ударов от бортов, представленный в Разделе 6.02.
Во-первых, вы представляете, в какую точку прицельного шара попадёт биток (точка А).
Далее вы высказываете предположение относительно того, как пойдёт линия прицеливания, для определения точки взаимодействия с бортом (точка В).
Затем вы находите воображаемую точку С, которая является смежной для точки А.
Затем вы проверяете равенство расстояний от точек А и С до высоты, опущенной из точки В.
Если они равны, то направление прицеливания и точка взаимодействия с бортом В выбраны правильно.
Если расстояния не равны, вы должны внести корректировку в прицеливание как вы это делали, используя Метод равных отрезков, представленный в Разделе 6.02.
Если вы используете кий для визуализации лини прицеливания и разместили наклейку в точке В, то держа кий вдоль линии прицеливания и глядя вдоль высоты, опущенной из точки В,
становится легко увидеть расстояния между точками А и С и высотой (смотри NV 6.5).
Для сравнения отрезков данным методом использовать алмазы довольно сложно.
Тем не менее, вам не нужно точно измерить расстояния, вам нужно лишь увидеть равны они или нет.
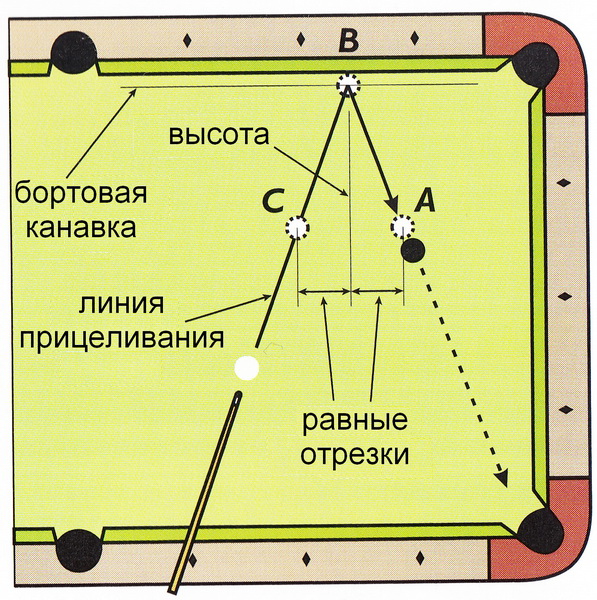
NV 6.5 Метод равных отрезков для абриколей
Раздел 6.04 Эффекты скорости
Угол отражения для ударов от бортов и абриколей будет отличаться от угла падения из-за влияния скорости, винта и эффектов резки. Важно быть в курсе всех этих эффектов, потому что в противном случае от методов прицеливания ударов от бортов, представленных в предыдущих двух разделах, мало пользы. Все эти методы основаны на том, что угол отражения в точности равен углу падения. Понимание принципов, представленных в данном разделе, а также Разделах 6.05 и 6.06, поможет вам в случае необходимости внести коррективы в методы прицеливания. С помощью этих методов, вы сможете уверенно выполнять широкий спектр ударов от бортов и абриколей.
Основным фактором, влияющим на угол отражения для ударов от борта, является скорость.
Как указано в Принципе 6.6, с увеличением скорости угол отражения уменьшается (смотри Рисунок 6.16).
Это явление обусловлено отбросом шара назад от борта, который вызван боковым сжатием борта (смотри Рисунок 6.17 и HSV 6.1).
Боковое сжатие происходит в результате действия сил, направление которых противоположно направлению движения шара, тем самым уменьшая угол отражения.
Угол отражения "укорачивается".
При ударе от борта и абриколе, увеличение силы удара приводит к уменьшению угла отражения (смотри Рисунок 6.16 и NV 6.6).
- При тихих ударах, угол отражения наоборот увеличивается (смотри Принцип 6.7).
- Эффект наиболее выражен для среднего угла подхода к борту (от 20° до 50°). Наибольший отброс назад происходит при угле около 30°.
- Когда прицельный шар стоит близко к борту, угол отражения ещё меньше (смотри Принцип 6.8).

NV 6.6 Эффект скорости при ударе от борта

HSV 6.1 Деформация борта во время сильного удара
На Рисунке 6.18 показан пример, где при исполнении удара от борта вы можете использовать эффект отброса назад в своих интересах.
Полосатые шары препятствуют прямому попаданию сплошного шара в лузу.
Единственный выход - это попытаться выполнить дуплет или отыграться.
Полосатый шар, помеченный как "шар-препятствие", делает невозможным исполнение такого дуплета, где угол отражения равен углу падения.
Тем не менее, возможным решением является выполнить удар мимо шара-препятствия с достаточной силой, чтобы угол отражения был меньше угла падения, как показано на рисунке.
Насколько сильным должен быть удар поможет почувствовать интуиция, которая может прийти только с большой практикой и опытом.

Как указано в Принципе 6.7, когда скорость снижается, угол отражения увеличивается (смотри Рисунок 6.19).
Основная причина это эффекта - это образующийся у шара естественный накат.
Когда шар отражается от борта с верхним винтом, отражённая траектория шара образует дугу из-за вращательного момента, увеличивая тем самым угол отражения.
Втора причина увеличения эффективного угла отражения - это недостаточная отражаемость
(технический фактор, называемый коэффициентом восстановления и представленный в TP 6.3).
Шар, попадая в борт, теряет часть своей скорости в направлении, перпендикулярном борту, так как борт не идеально упругий (то есть, борт не идеально отражает шары).
Этот эффект приводит к увеличению угла отражения.
Угол отражения зовётся "удлинённым".
Для дуплетов и абриколей снижение скорости шара приводит к увеличению угла отражения от борта (смотри Рисунок 6.19 и NV 6.7).
- При увеличении силы удара, угол отражения уменьшается (см Принцип 6.6).
- Дуга образуется по причине вращательного момента, связанного с естественным накатом. Угол отражения также несколько увеличивается из-за недостаточной восстанавливаемости борта (смотри TP 6.3).
- Эффект более выражен для средних значений угла подхода. Наибольшее отклонение шара наблюдается при угле 45°, когда направление наката перпендикулярно направлению отражения шара от борта.
- Когда прицельный шар находится близко к борту дуговая траектория меньше проявляется (смотри Принцип 6.8).
- Для абриколей нижний винт может быть использован, чтобы уменьшить этот эффект, а накат - наоборот, чтобы усилить (смотри HSV 6.2 - 6.5).

NV 6.7 Эффект медленной скорости
HSV 6.2 Абриколь с накатом
HSV 6.3 Абриколь с оттяжкой
HSV 6.4 Абриколь с нормальным накатом
HSV 6.5 Абриколь с клапштосом

| TP 6.3 Увеличение угла отражения от борта из-за коэффициента восстановления борта |
На Рисунке 6.20 показан пример дуплета, где вы используете эффект низкой скорости в ваших интересах.
Полосатые шары препятствуют прямому попаданию сплошного шара в лузу.
Единственный выход - это попытаться выполнить дуплет или отыграться.
Полосатый шар, помеченный как "шар-препятствие", делает невозможным исполнение такого дуплета, где угол отражения равен углу падения.
Тем не менее, возможным решением является выполнить достаточно тихий удар мимо шара-препятствия,
чтобы угол отражения был меньше угла падения, как показано на рисунке.
Насколько тихим должен быть удар опять же поможет почувствовать интуиция, которая может прийти только с большой практикой и опытом.

Степень увеличения или уменьшения угла отражения, вызванного эффектом отброса шара назад и эффектом наката, также зависит от того,
насколько близко прицельный шар находится от борта (смотри Принцип 6.8).
Чем ближе прицельный шар стоит к борту, тем меньше у него времени на то, чтобы развить накат.
Таким образом, дуга будет не настолько крутая (смотри Рисунок 6.21).
Если выполняется дуплет и прицельный шар стоит близко к борту, то угол отражения будет меньше ожидаемого (смотри Рисунок 6.21).
- Прицельный шар не имеет достаточного расстояния, чтобы развить накат (смотри Принцип 6.7). Вместо этого, прицельный шар скользит к борту, в результате чего угол отражения может немного уменьшаться. Фактически, угол отражения может быть укорочен и в результате бортового отброса назад (смотри Принцип 6.6).
- Для абриколей накат может быть использован, чтобы нейтрализовать данный эффект.

В Принципе 6.6 говорится, что с возрастанием скорости возрастает и степень отброса шара от борта,
а в Принципе 6.7 говорится, что с уменьшением скорости увеличивается размер дуги.
К счастью, как указано в Принцип 6.9 и показано на Рисунке 6.22, при ударе средней силы и без бокового винта, шар
отражается от борта по ожидаемой траектории, где угол отражения равен углу падения.
Таким образом, для забития дуплетов или абриколей, используя среднюю скорость и не используя бокового винта,
прекрасно работают методы прицеливания, представленные в Разделах 1.02 и 1.03.
Опять же, чёткое понимание, с какой силой произвести удар, приходит только с практикой.
Используя соответствующую среднюю силу удара, эффекты отброса от борта и дуги (смотри Принципы 6.6 и 6.7) погашают друг друга, в результате чего удар полностью соответствует теоретическим посылам, согласно которым угол отражения равен углу падения (смотри Рисунок 6.22).
- Если шар, отражающийся от борта, имеет боковое вращение, то угол отражения будет смещаться в сторону действия винта (смотри следующий раздел).

Далее
Chapter 6. Bank and Kick Shots (2)
Section 6.03 Kick-shot aiming methods
With a kick shot, the cue ball rebounds off a rail before striking the object ball.
If the target ball is close to a pocket, as shown in Figure 6.12, the bank-shot methods presented in the previous section can be
used to aim the shot, except that you plan the path of the cue ball instead of the object ball.
The main difference is that you have more control over the English of the banking ball (the cue ball).
The good news concerning this fact is that you do not need to worry about cut shot effects (see Section 6.06).
However, you must be very careful not to put unintentional English on the cue ball (see Section 6.05).

Fоr kick shots where the object ball is close to the banking rail or far from the target pocket, the following methods are more appropriate.
The first method, called the mirror-image kick-shot method, is illustrated in Figure 6.13 and summarized in Principle 6.5.
To use the method, you simply visualize the mirror image of the object ball reflected about the rail groove, and aim at the imaginary mirror-image ball.
The mirror-image ball can be difficult to visualize when the object ball is far from the rail; but when it is closer, the method is fairly easy to apply.
When you get comfortable with and good at visualizing the mirror-image ball, you can even plan for the desired amount of cut
angle you want between the cue ball and object ball, by aiming with the appropriate cut angle at the mirror-image ball.
Figure 6.14 illustrates how this is done.
Notice that the direction of the cut angle is reversed in the mirror image.
To make the object ball in the pocket, the cue ball strikes to the right of center of the object ball.
In the mirror image, you need to aim to the left of center of the mirror-image with the same amount of cut angle.


For a medium speed kick shot with no English, you can aim directly at the mirror image of the object ball reflected about the rail groove (see Figure 6.13, Figure 6.14, and NV 6.4).
- This principle is a direct consequence of Principle 6.1 (see TP 6.2).
- You need to adjust your aim at fast or slow speeds (see Section 6.04) and when English is used (see Section 6.05).
NV 6.4 Mirror-image kick-shot method

Another method for aiming kick shots is illustrated in Figure 6.15.
It is called the equal separation-distance kick-shot method.
It is applied in very much the same way as the equal rail-distance bank-shot method presented in Section 6.02.
First, you visualize where you want the cue ball to hit the object ball (position A).
Next, you guess at an aiming line to define the rail-impact aim point (position B).
Then, you imagine position С of the cue ball adjacent to position A.
Next, you check the distances of positions A and С from the centerline through position B.
If they are equal, the aim direction and rail-impact point В are correct.
If the distances are unequal, you need to adjust your aim, just as with the equal rail-distance method, presented in Section 6.02.
If you use your cue stick to visualize the aiming line with the tip at point B, it is easier to visualize the distances between the centerline and
point A and С by keeping the cue stick along the aiming line, and by looking down the centerline (see NV 6.5).
It is difficult to use the rail diamonds to help compare the distances with this method.
However, you do not need to measure the distances but just be able to visualize whether or not they are equal.

NV 6.5 Equal separation-distance kick-shot method
Section 6.04 Speed effects
The rebound angle for kick and bank shots will differ from the approach angle due to speed, spin, and cut-angle effects. It is important to be aware of all of these effects; otherwise, the bank aiming-methods presented in the previous two sections will not be of much use. All of these methods assume that the rebound angle is exactly equal to the approach angle. By understanding the principles presented in this section, Section 6.5 and Section 6.06, you will be able to make adjustments to the bank aiming-method results where appropriate. With these techniques, you will be able to confidently execute a wide variety of kick and bank shots.
The most fundamental factor affecting a kick or bank shot rebound angle is speed.
As summarized by Principle 6.6, the rebound angle decreases when the speed increases (see Figure 6.16).
This phenomenon is due to what I call rail throwback, which is caused by sideways compression of the rail (see Figure 6.17 and HSV 6.1).
The sideways compression results in sideways forces that oppose the ball's sideways motion, thereby reducing the rebound angle.
The rebound angle is said to be "shortened".
With kick and bank shots, higher speed results in a smaller rebound angle (see Figure 6.16 and NV 6.6).
- At slower speeds, the rebound angle increases (see Principle 6.7).
- The effect is most pronounced for medium-angle bank shots, especially where the approach angle is between about 20° and 50°. The largest throwback occurs at about 30°.
- When the object ball is closer to the rail to begin with, the rebound angle can be even smaller (see Principle 6.8).

NV 6.6 Bank high-speed effect

HSV 6.1 Rail deformation during high-speed bank
Figure 6.18 shows an example where you can use the high-speed throwback effect to your advantage to execute a bank shot.
Due to the stripes on the table the solid has no direct path to a pocket.
The only option is to try to execute a bank shot or to play a safety.
The stripe labeled as "obstacle ball" makes it impossible to execute an equal rail distance bank shot
where the rebound angle is the same as the approach angle.
However, a possible solution is to shoot clear of the obstacle ball with enough speed so the rebound angle is smaller than
the approach angle, as shown in the figure.
The tough part is having a feel for how much speed to use.
This intuition can come only with a great deal of practice and experience, but it does help to be aware of the facts presented in Principle 6.6.

As summarized by Principle 6.7, the rebound angle increases when the speed decreases (see Figure 6.19).
The primary cause for this effect is topspin resulting from normal roll of the banking ball.
When a ball bounces off a rail with topspin, the rebound path curves due to the angular momentum of the spin, effectively increasing the rebound angle.
A secondary cause for the larger effective rebound angle is rail-rebound inefficiency
(described by a technical factor called the coefficient of restitution, presented in TP 6.3).
The banked ball loses some of its speed in the direction perpendicular to the rail, because the rail is not perfectly elastic (i.e., the rail does not rebound perfectly).
This effect results in a larger rebound angle.
The rebound angle is said to be "lengthened".
With kick and bank shots, slower speed results in a larger rebound angle (see Figure 6.19 and NV 6.7).
- At faster speeds, the rebound angle decreases (see Principle 6.6).
- The rebound path curves due to the topspin momentum of the banked ball due to normal roll. The rebound angle is also increased slightly due to rail rebound inefficiency (see TP 6.3).
- The effect is more pronounced for medium approach angles. The largest deflection occurs at about 45°, where the forward-roll direction is perpendicular to the rebound direction.
- When the object ball is close to the rail to begin with, there is not as much curve (see Principle 6.8).
- For kick shots, bottom spin can be used to help reduce this effect, and topspin can increase the effect (see HSV 6.2 through HSV 6.5).

NV 6.7 Bank low-speed effect
HSV 6.2 Cue ball kicked off a rail at an angle, with top spin
HSV 6.3 Cue ball kicked off a rail at an angle, with bottom spin
HSV 6.4 Cue ball kicked off a rail at an angle, with normal roll
HSV 6.5 Cue ball kicked off a rail at an angle, with stun

| TP 6.3 Increase in bank rebound angle due to the rail coefficient of restitution |
Figure 6.20 shows an example where you can use the bank low-speed-roll effect to your advantage to execute a bank shot.
Due to the stripes on the table the solid has no direct path to a pocket.
The only option is to try to execute a bank shot or to play a safety.
The stripe labeled as "obstacle ball" makes it impossible to execute an equal rail-distance bank shot where the rebound angle is the same as the approach angle.
However, a possible solution is to shoot clear of the obstacle ball with slow enough speed so the rebound angle
is larger than the approach angle, as shown in the figure.
Again, the tough part is having a feel for how little speed to use.
This intuition can come only with a great deal of practice and experience, but it does help to be aware of the facts presented in Principle 6.7.

The amount of increase or decrease in the rebound angle due to rail throwback and roll effects is also affected by how close the object
ball is to the rail to begin with (see Principle 6.8).
The closer the object ball is to the rail, the less time it has to develop forward roll.
Therefore, the rebound path does not curve as much (see Figure 6.21).
When banking an object ball that is close to a rail, the rebound angle will be smaller than expected (see Figure 6.21).
- The object ball does not have enough distance to build up roll (see Principle 6.7). Instead, the object ball slides into the rail and there is little or no increase in rebound angle. In fact, the rebound angle can even be shortened due to rail throwback (see Principle 6.6).
- For kick shots, topspin can be used to counteract this effect.

Principle 6.6 showed that as the speed of a banked ball increases, the amount of throwback increases;
and Principle 6.7 showed that as the speed decreases, the amount of rebound curve increases.
Fortunately, as summarized in Principle 6.9 and shown in Figure 6.22, with medium speed and no sidespin, the banked ball does
rebound off the rail as expected where the rebound angle is equal to the approach angle.
Therefore, for balls banked or kicked with medium speed and no sidespin, the aiming methods presented in Section 1.02 and Section 1.03 work perfectly.
Again, knowing how much speed to use comes only with practice.
With an appropriate medium speed, the bank throwback and roll curve effects (see Principle 6.6 and Principle 6.7) cancel, resulting in a bank shot that agrees with the theoretical bank geometry, where the rebound angle is equal to the approach angle (see Figure 6.22).
- If the ball hitting the rail has sidespin, the rebound angle will deflect in the direction of the spin (see the next section).
