Глава 3. Выполнение основных ударов (4)
Раздел 3.07 Пределы погрешностей ударов
Используя принципы и графики, представленные в предыдущем разделе, становится возможным предсказать допустимые пределы погрешности для разных дистанций от лузы
(смотри TP 3.10 и TP 3.11).
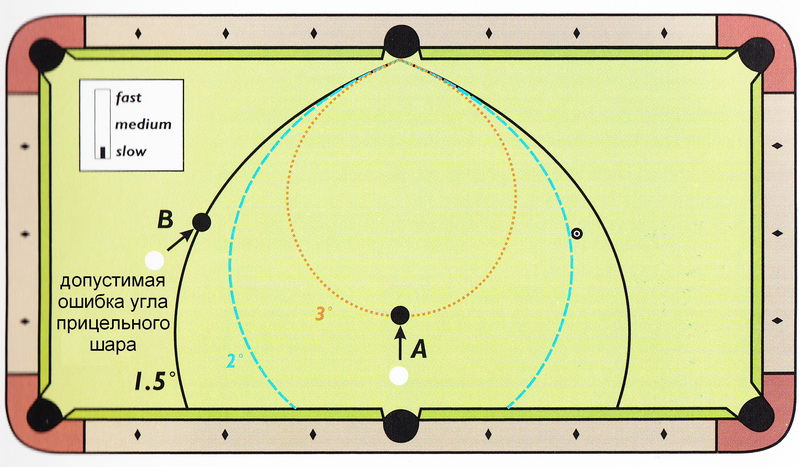
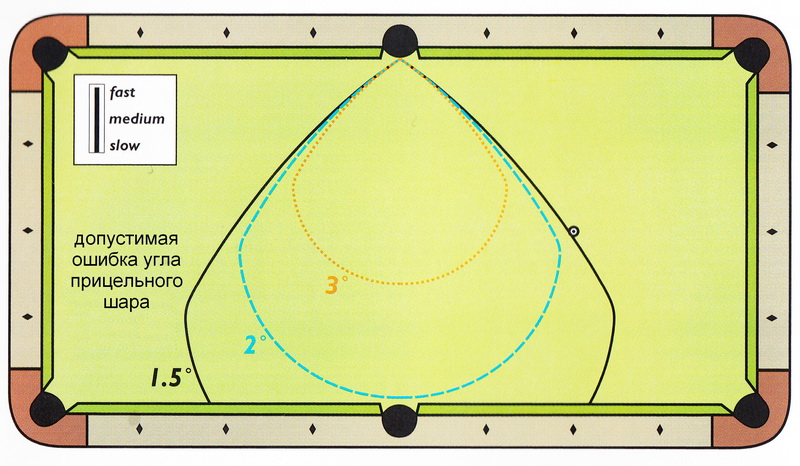
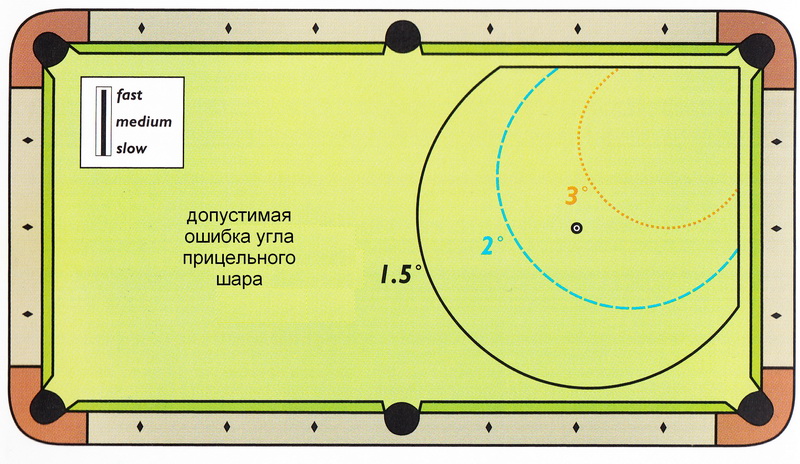
На Рисунках 3.40 - 3.43 представлены результаты для средней и угловой лузы для тихих и сильных ударов.
Ошибка угла прицельного шара является мерой необходимой точности ударов.
Например, предел погрешности 3° означает, что прицельный шар может быть забит в лузу даже если ошибка целевой линии составит целых 3°.
На рисунках, если прицельный шар находится в пределах одной из кривых, то это значит, из этого положения прицельный шар
будет всё ещё забит в лузу, пока ошибка угла не превысит заданное значение.
Эти рисунки учитывают и эффект расстояния до лузы и значение эффективного размера луз.
Все выводы и результаты, представленные в предыдущем разделе, можно увидеть наглядно в этих рисунках.
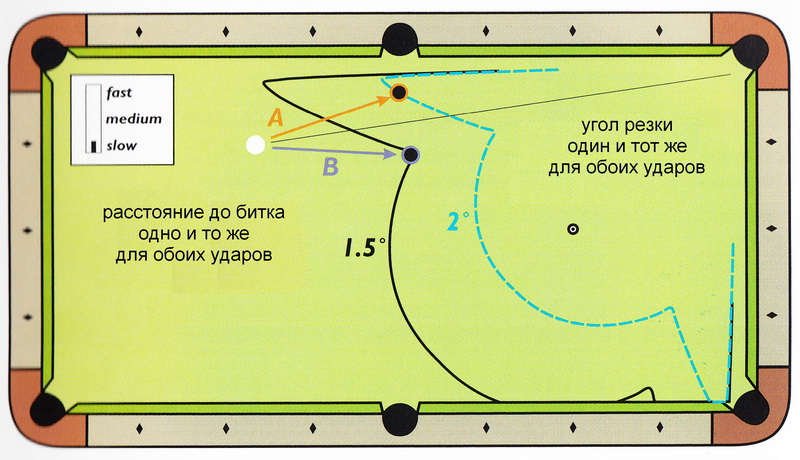
Два удара (А и В), показанные на Рисунке 3.40, помогают сделать вам определённые выводы.
Оба удара без резки, и оба удара выполняются на одинаковом расстоянии от лузы.
Тем не менее, пределы погрешности весьма различны: 3° для удара A и 1.5° для удара B.
Таким образом, удар В будет в два раза сложнее успешно выполнить, нежели удар А.

| TP 3.10 Области пределов погрешности для тихих ударов |
Рисунки 3.44 и 3.45 иллюстрируют, как приведённые выше области могут помочь вам в выборе удара.
На Рисунке 3.44 показаны две различные позиции шаров, причём обе имеют одинаковый угол резки и одинаковое расстояние до угловой лузы.
Вопрос заключается в том, какой из этих ударов будет проще, предполагая, что после любого удара можно сделать одинаково хороший выход для следующего удара.
Неопытный игрок может подумать, что оба удара одинаково лёгкие (или сложные).
Однако, как видно из графиков, удар А будет легче выполнить успешно, потому что его предел погрешности 2°, вместо 1.5° для удара В.
Это означает, что удар А на 33% легче удара В.
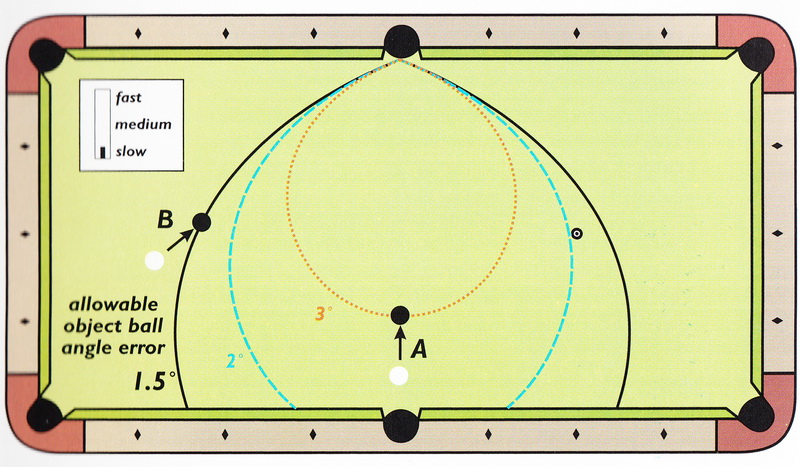
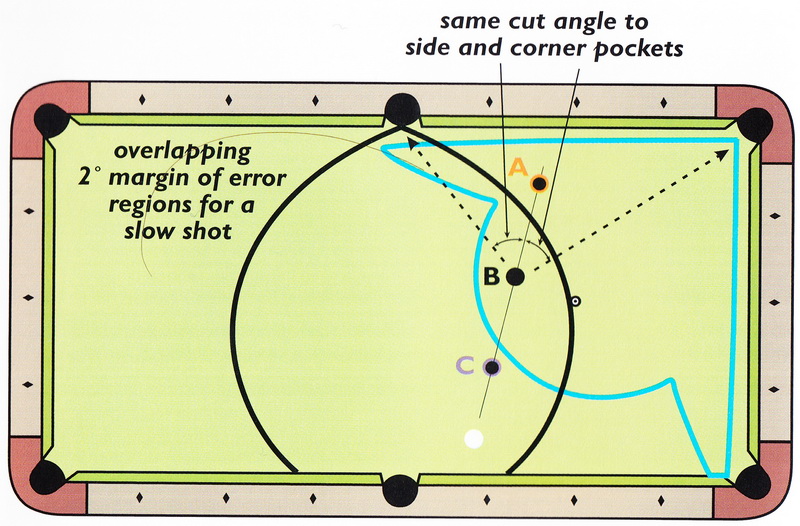
На Рисунке 3.45 приведён пример, когда вам для данного расположения битка нужно сделать выбор в какую лузу нанести удар: в среднюю или угловую.
Показаны три различных варианта расположения прицельного шара (А, В и С).
Для каждого из трёх ударов угол резки в среднюю лузу точно такой же как и угол резки в угловую.
Тогда как принять решение, в какую лузу бить?
С помощью областей пределов погрешности ответ ясен для каждой позиции прицельного шара.
Позиция А находится в области допустимого предела погрешности угловой лузы и за пределами области средней лузы - поэтому очевидным выбором будет удар в угловую лузу.
Позиция В находится в обеих областях и одинаково близка к границе областей, таким образом, удар что в угловую что в среднюю лузы имеет одинаковый уровень трудности, и
вы должны выбрать для себя тот вариант, который кажется вам наиболее удобен.
Позиция С расположена очень хорошо в области пределов погрешности для средней лузы и за пределами области угловой лузы, таким образом удар в среднюю лузу - очевидный выбор.

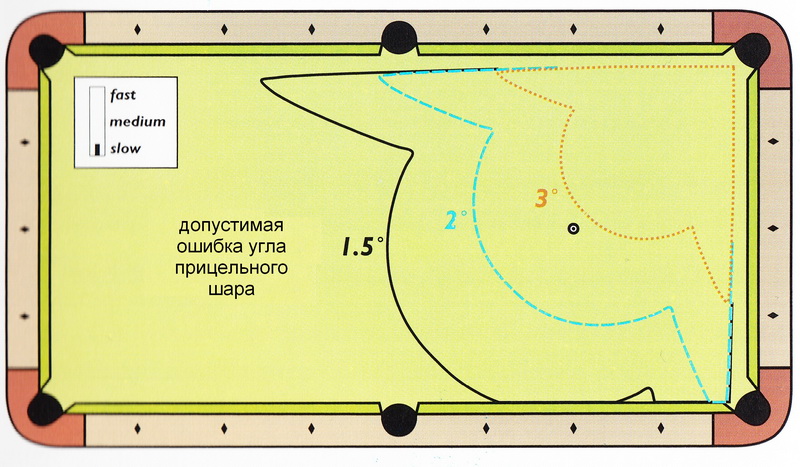
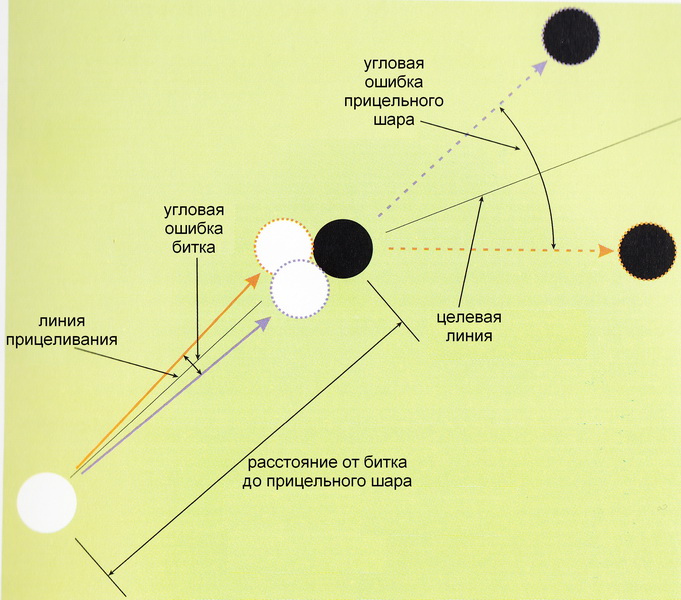
Области пределов погрешностей, нарисованные выше, описывают угловую ошибку прицельного шара, то есть, насколько близко путь прицельного шара должен проходить от целевой линии.
Как показано на Рисунке 3.46, допустимая угловая ошибка битка, измеренная относительного линии прицеливания, должна быть ещё намного меньше.
Кроме того, сложность удара увеличивается с увеличением расстояния между лузой и прицельным шаром; с увеличением расстояния между битком и прицельным шаром (смотри Принцип 3.16);
а также с увеличением угла резки (смотри Принцип 3.17).
Если все эти три величины увеличиваются, то и сложность удара увеличивается, а допустимый предел погрешности резко уменьшается.
Детальный анализ и графики, демонстрирующие влияние расстояния до битка, угла резки и ошибки в угле резки вы найдёте в TP 3.12.
Допустимый предел погрешности резко уменьшается с увеличением расстояния между битком и прицельным шаром (смотри TP 3.12).
- Предел погрешности также уменьшается с увеличением расстояния от прицельного шара до лузы (смотри Принцип 3.8).
- Предел погрешности также уменьшается с увеличением угла резки (смотри Принцип 3.17).
Допустимый предел погрешности резко уменьшается с возрастанием угла резки (смотри TP 3.12).
- Предел погрешности также уменьшается с возрастанием расстояния от прицельного шара до лузы (смотри Принцип 3.8)
- Предел погрешности также уменьшается с возрастанием расстояния от битка до прицельного шара (смотри Принцип 3.16)

| TP 3.12 Зависимость угловой ошибки прицельного шара от угла резки |
Далее
Chapter 3. Executing Basic Shots (4)
Section 3.07 Shot margins of error
Using the concepts and graphs presented in the previous section, the allowable margin of error for different distances
from the pocket can be predicted (see TP 3.10 and TP 3.11).
Figure 3.40 through Figure 3.43 are plots of the results for side and corner pockets at slow and fast speeds.
The object-ball angle error is a measure of the required shooting accuracy.
For example, a margin of error of 3° implies that the object ball can be pocketed with an error in the target-line angle of as much as 3°.
In the figures, if the object ball lies on or within one of the angle-error curves,
then the object ball can be pocketed as long as the shot angle error is no more than the value reported.
These plots combine the distance-to-the-pocket effects with the target-size effects into one illustration.
All conclusions and results presented In the previous section can be seen graphically in these plots.
The two shots (A and B) illustrated in Figure 3.40 help illustrate the type of conclusions you can make.
Neither shot has a cut angle, and both are the same distance from the pocket.
However, the object-ball margins of error are quite different: 3° for shot A and 1.5° for shot B.
Therefore, shot В would be twice as difficult as shot A to execute successfully.


| TP 3.10 Pocket margin-of-error regions for a slow shot |
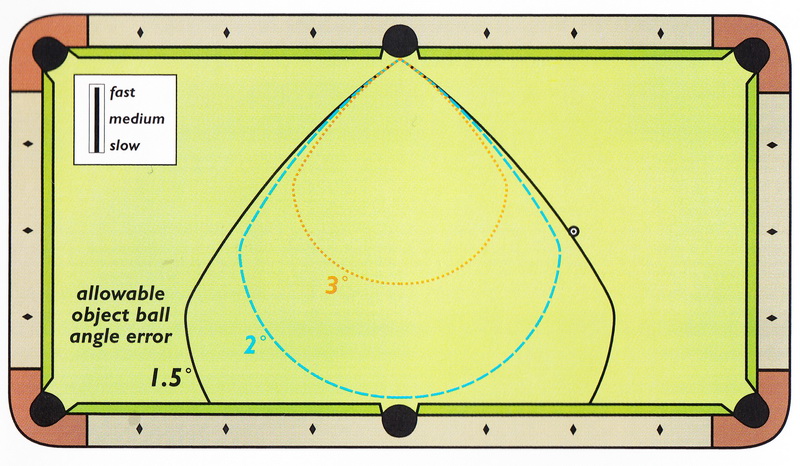
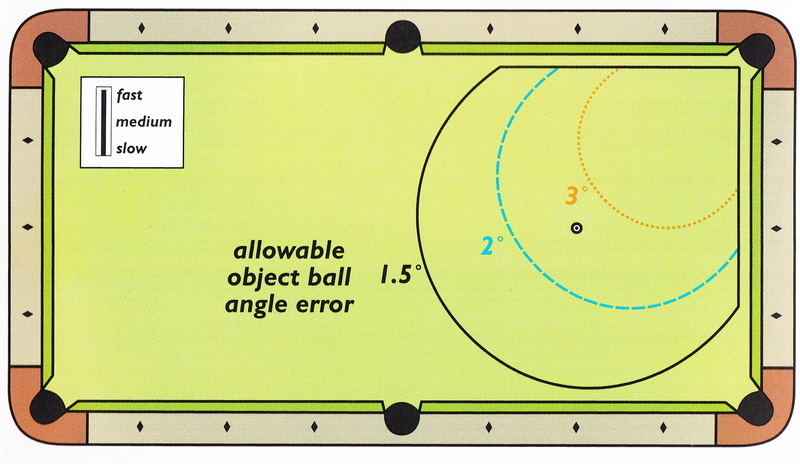
Figure 3.44 and Figure 3.45 illustrate how the figures above can be useful in helping you understand shot selection.
Figure 3.44 shows two different object ball positions, both of which have the same cut angle and distance to the corner pocket.
The question is which shot would be easier, assuming that either shot would create equally good position for the next shot.
An inexperienced player might think each shot is equally easy (or difficult).
However, as shown by the curves, shot A would be easier to execute because its margin of error is 2° versus 1.5° for shot B.
That means shot A would be 33% easier than shot B.
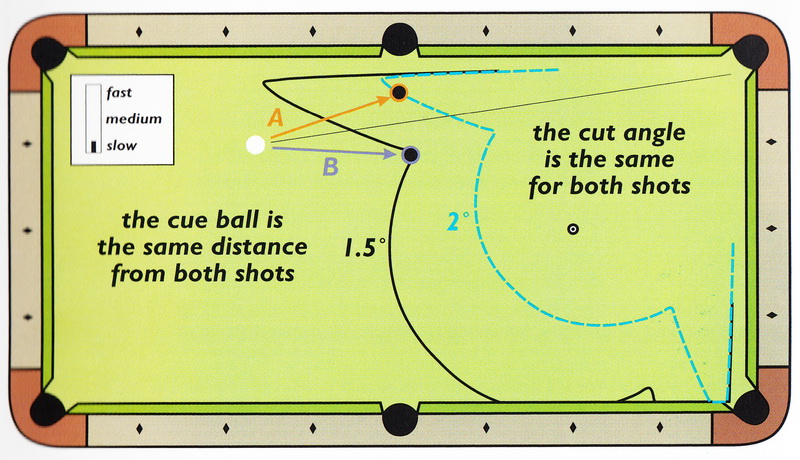
Figure 3.45 shows an example where you need to decide between a corner- or side-pocket shot for a given object-ball location.
Three different object-ball locations (A, B, and C) are shown.
For each of these shots, the cut angle to the side pocket is the same as the cut angle to the corner pocket.
Then how do you decide which pocket is easier to shoot at?
With the margin-of-error regions shown, the answer is clear for each object-ball position.
Position A is within the corner pocket region and outside of the side pocket region; therefore, the corner pocket is the clear best choice.
Position В is within both regions and equally close to each region boundary;
in this case, both pockets have the same level of difficulty, so you should pick the one that feels most comfortable.
Position С is well within the side-pocket region and just outside of the corner-pocket region; therefore, the side pocket is the clear best choice.
The margin-of-error region plots above concern object-ball angle error, which corresponds to how close the object-ball path needs to be to the target line.
As Figure 3.46 illustrates, the allowable cue-ball angle error, measured relative to the desired aiming line, needs to be even more accurate than that.
Furthermore, a shot’s difficulty increases as the distance between the object ball and the pocket increases,
as the distance from the cue ball to the object ball increases (see Principle 3.16), and as the cut angle increases (see Principle 3.17).
If all three measures increase together, the difficulty level increases and your margin of error decreases dramatically.
A detailed analysis and plots showing the effects of cue ball distance, cut angle, and cut-angle error can be found in TP 3.12.

The margin of error decreases dramatically as the distance between the cue ball and object ball increases (see TP 3.12).
- The margin of error also decreases with distance between the object ball and the target (see Principle 3.8).
- The margin of error also decreases with cut angle (see Principle 3.17).
The margin of error decreases dramatically as the cut angle increases (see TP 3.12).
- The margin of error also decreases with distance between the object ball and the target (see Principle 3.8).
- The margin of error also decreases with distance between the cue ball and object ball (see Principle 3.16).

| TP 3.12 Object ball angle error, based on cut angle |