TP 3.4 Зависимость предела погрешности от расстояния

Радиус шара: R=1.125
φ: Угол резки
θ: Угол отклонения прицельного шара от линии прицеливания
d: Расстояние от битка до прецельного шара
Предполагается, что d>>R

В правой нижней части рисунка выше: приравнивание вертикальных составляющих дает:

Следовательно:

Пример: Какова допустимая погрешность угла прицельного шара и требуемая точность угла битка для следующих условий? Медленный удар с углом резки 30° (удар в пол-шара). Удар выполняется в угловую лузу. Угол к лузе 0°. Дистанция между битком и прицельным шаром около 4 алмазов (4.5 фута = 137.16 см)

Из Рисунка 3.41 (из книги) примерно допустимый угол ошибки прицельного шара равен:

Расстояние между битком и прицельным шаром:

и угол резки для удара в пол-шара равен:

Следовательно, требуемая точность угла битка равна:

начальное приближение:

даёт:

Таким образом, предел погрешности для битка для этого удара очень мал (меньше чем 0.1°)

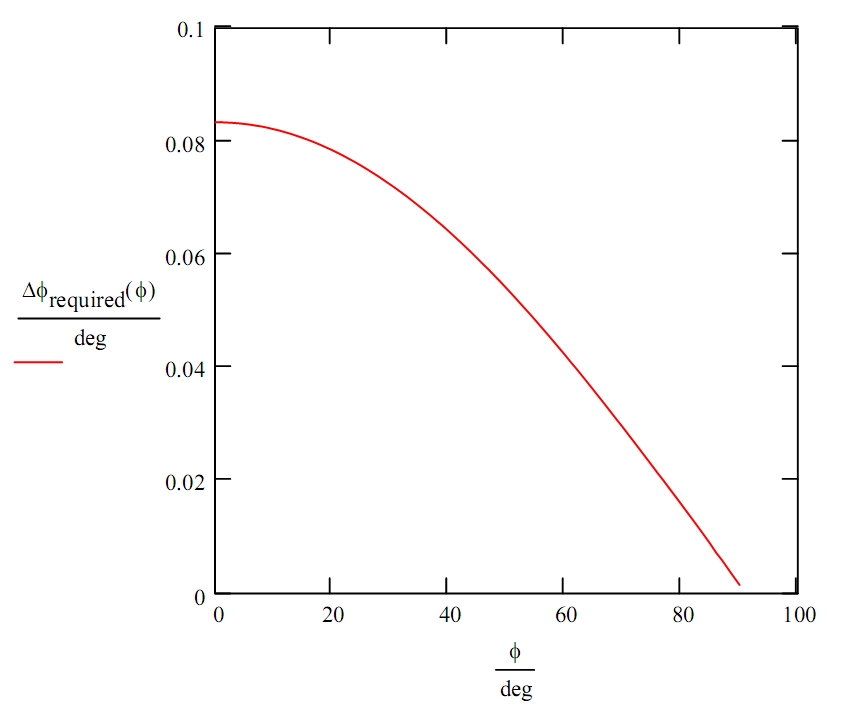
Допустимый предел погрешности битка для различных углов резки:

начальное приближение:

Удар "в лоб" в 1.15 раза (15%) легче, чем удар на резке 30°

Удар "в лоб" в 1.97 раз (97%) легче, чем удар на резке 60°

TP 3.4 Margin of error based on distance and cut angle

ball radius: R := 1.125
φ: cut angle
θ: object ball leaving angle
d: distance between cue and object balls
Assume: d >> R

From the bottom right portion of the figure above, equating the vertical components of the loop (perpendicular to the horizontal project line) gives:

Therefore,

Example: What is the allowable object ball (OB) angle error and required cue ball (CB) angle accuracy for a slow, 30-degree cut angle (half-ball hit) shot straight into a corner pocket (i.e., the angle to the pocket is 0 degrees) if the distances between the CB and OB and the OB and pocket are both about 4 diamonds (about 4.5' = 54" on a 9' table)?

From Figure 3.41 in the book, the approximate allowable object ball angle error is:

The distance between the CB and OB is:

and the cut angle for a half-ball hit is:

Therefore, the required cue ball angle accuracy is:

initial guess:

Given

So the margin for error for the CB in this shot is very small (less than 0.1 degree!)

Allowable cue ball margin for error for various cut angles for the example shot above:

initial guess

a straight-in shot is 1.15X (15%) easier than a 30 degree cut angle shot.

a straight-in shot is 1.97X (97%) easier than a 60 degree cut angle shot.